Problem Set 9: Gratings

Problem Set 9: Gratings#

A plane wave with a wavelength \(\lambda = 600 nm\) is incident onto an aperture that consists of a periodic set circular holes. Fig. 9 shows the aperture that consists of a 10 X 10 array of holes with diameters of \(10 \mu m\) and spacing of \(20 \mu m\). The aperture is followed by a lens with a focal length of f=10mm. Calculate the equation for the normalized irradiance at the focal plane of the lens. Use a computer to plot the 2D irradiance pattern.

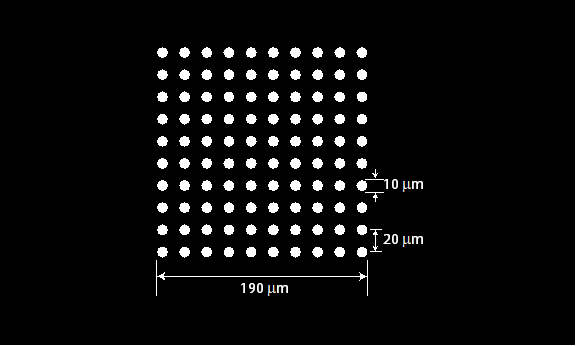
Fig. 9 Aperture consisting of a periodic set circular holes.#
What is the transmission function, \(t(x)\), of the grating if Fig. 10 shows a single grating period? The material has an index of refraction of n. Your answer should be in terms of \(\Lambda, d, \mathrm{rect}(x), \delta(x)\), and \(n\). Be sure to include the infinite periodicity of the grating (there should be a convolution in your answer).

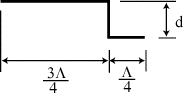
Fig. 10 Single period of the grating.#
A binary surface relief phase grating is designed such that if the incident beam is normally incident on the grating then the first diffraction order is transmitted through the substrate at an angle of \(10^\circ\) with respect to the surface normal. Use a wavelength of \(\lambda = 500 nm\).
1. What is the grating period?
2. How many orders are there, which are transmitted through the grating into air?
A binary surface relief phase grating is designed such that if the incident beam is normally incident on the grating then the first diffraction order is transmitted through the substrate at an angle of \(10^\circ\) with respect to the surface normal. The grating is designed such that the m=0 order has no power (\(\eta_0 = 0\)). Use a wavelength of \(\lambda = 500 nm\), a refractive index of n=1.5, and a 50% fill factor (F=0.5).
1. What is the thickness of the grating?
2. What are the normalized efficiencies of all of the supported orders? Assume that the Fraunhofer diffraction integral is valid.
An index grating is illuminated with a laser beam that has a wavelength of \(\lambda = 600 nm\) and an intensity pattern of \(I=5 \exp{\left(-\left(\frac{r}{10^{-3}}\right)^2\right)}\frac{mW}{m^2}\). The grating has a period of \(\Lambda= 50 \mu m\), is fabricated out of glass that has a refractive index of n=1.6, has a depth of d=200 nm, a fill factor of F=3/4 (see Fig. 10), and a width of W=1mm. What is the electric field for the m=1 order at z=10 m away from the grating?