15. Telescopes

15.1. Types of telescopes

Object and image are both at infinity (collimated light in, collimated light out).

There are 2 main configurations: Kepler, and Galilean (see Fig. 15.1).

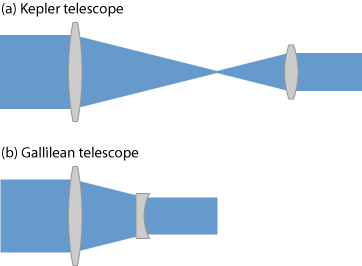
Fig. 15.1 Kepler vs Galilean telescopes.

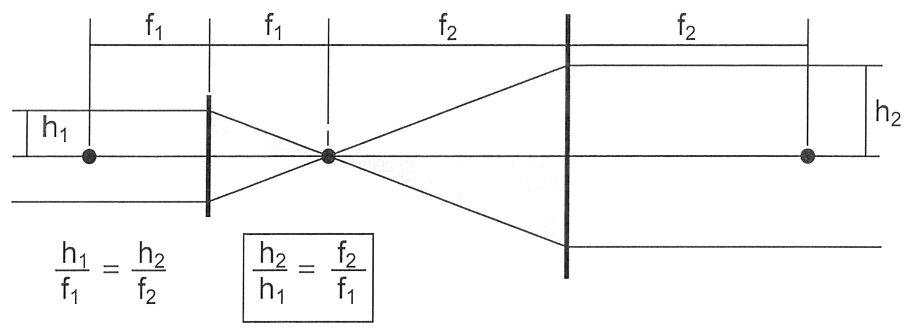
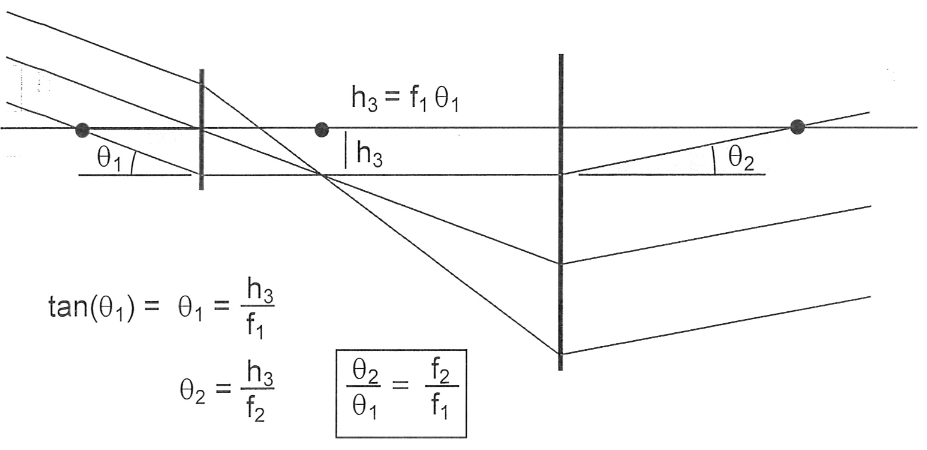
In Kepler telescopes, both \(f_1\) and \(f_2\) are positive lenses with the distance between them \(D = f_1 + f_2\). Galilean telescopes, on the other hand, have \(f_1\) as a positive lens and \(f_2\) as a negative lens. The distance \(D\) between is still \(D = f_1 + f_2\); in this case, however, the distance is shorter (since one of the lenses is negative).

Since there is no focus, we will use angular magnification:

(15.1)\[\begin{equation} M_{ang} = \frac{\tan \theta '}{\tan \theta} = - \frac{F_1}{F_2} \end{equation}\]

Modern astronomical telescopes are actually really large cameras. The goal of a telescope is to separate two closely spaced, distant objects (such as two stars).

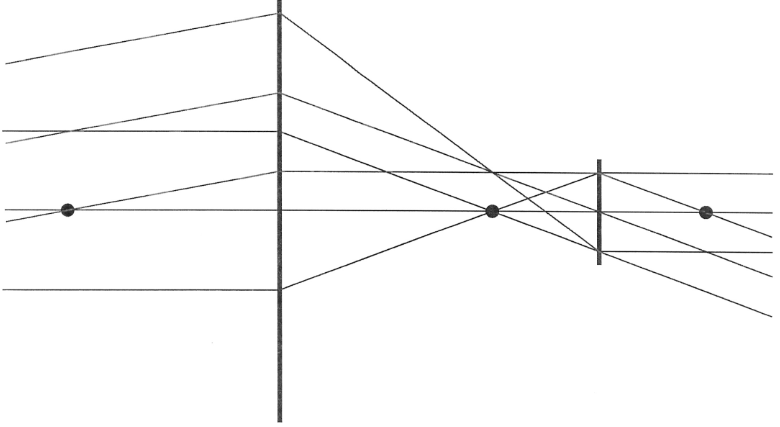
Let’s look at a circular aperture of an astronomical telescope. We’ll model it as a single perfect lens.

Fig. 15.2 Single perfect lens.

At the focal plane:

(15.2)\[\begin{align} E(x,y) &= \mathfrak{F} \left. \left\{ \mathrm{circ} \left( \frac{r}{D/2} \right) \right\} \right| _{f_r = r / \lambda f} \\ &= E_0 \left[ 2 \frac{J_1 ( 2 \pi \frac{D}{2} f_x )}{ 2 \pi \frac{D}{2} f_x } \right] \\ &= E_0 \left[ 2 \frac{J_1 ( 2 \pi \frac{D}{2} \frac{r}{\lambda f} )}{ 2 \pi \frac{D}{2} \frac{r}{\lambda f} } \right] \end{align}\]

15.2. Irradiance pattern

The irradiance pattern is

(15.3)\[\begin{equation} I = I_0 \left[ 2 \frac{ J_1 ( \pi D \frac{r}{\lambda f} ) }{ \pi D \frac{r}{\lambda f} } \right] ^2 \end{equation}\]

Show code cell source Hide code cell source

import numpy as np
from scipy.special import jv
import matplotlib.pyplot as plt

plt.subplots(figsize=(10,6))
a = np.linspace(-4, 4, 1000)
D = 2
I0 = 1
I = I0 * (2 * jv(1, D * a) / (D * a)) ** 2
plt.plot(a, I)
plt.title("Irradiance Pattern")
plt.xlabel("Position (au)")
plt.ylabel("Intensity (normalized)")
plt.grid()
plt.show()

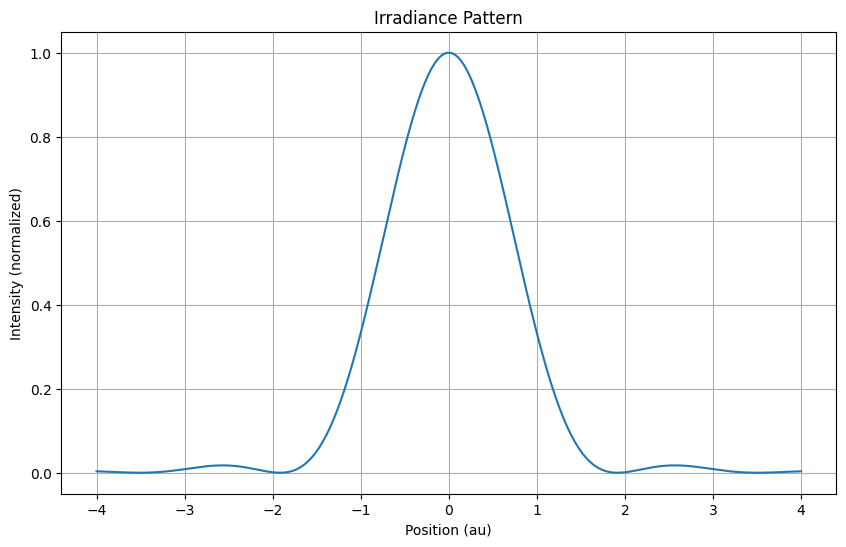
What is the diameter of the central lobe?

\[ J_1(3.832) = 0 \]

\[ \frac{\pi}{\lambda} \frac{D}{f} r = 3.832 \]

(15.4)\[\begin{align} r &= 3.832 \frac{\lambda}{\pi} \frac{f}{D} \\ &= \frac{3.832}{\pi} \lambda \frac{f}{D} \\ d = 2 r &= 2 \left( \frac{3.832}{\pi} \right) \lambda f_\# \\ d &= 2.44 \lambda f_\# \end{align}\]

This is called the Airy Disk.

What if the incident beam has a different angle?

Plane wave equation:

(15.5)\[\begin{equation} E_i = \exp [ j k (\sin \theta y + \cos \theta z)] \end{equation}\]

If we use \(E_i = \exp [j k \sin \theta y] = \exp [j 2 \pi \frac{\sin \theta}{\lambda} y]\):

(15.6)\[\begin{equation} E(x, y) = \mathfrak{F} \left. \left\{ \exp[j k \sin \theta y] \mathrm{circ} \left( \frac{r}{D / 2} \right) \right\} \right| _{f_r = r / \lambda f} \\ \end{equation}\]

The pattern is the same; it is just shifted by

(15.7)\[\begin{align} f_{x0} &= \frac{\sin \theta}{y} \\ \frac{y_0}{\lambda f} &= \frac{\sin \theta}{\lambda} \\ y_0 &= \sin \theta f \approx \theta f \end{align}\]

This is the same as that predicted by the conjugate equation.

15.3. Rayleigh Criteria

Rayleigh Criteria

Two incoherent point sources are “barely resolved” by a diffraction-limited system with a circular aperture when the center of the Airy disk of one point falls exactly on the first zero of the diffraction pattern.

(15.8)\[\begin{align} \pi D \frac{r}{\lambda f} &= 3.83 \\ r &= 1.22 \lambda \frac{f}{D} \\ \end{align}\]

So, the resolvable separation is

(15.9)\[\begin{align} 1.22 \lambda \frac{f}{D} &= f \theta \\ \theta &= 1.22 \frac{\lambda}{D} \end{align}\]

Hence, the angular resolution is better with a larger diameter.

However, a standard ground telescope has a limit to the maximum resolution it can attain. This limitation is caused by turbulence in the air.

See the following websites:

• https://www.astronomynotes.com/telescop/s11.htm

Low turbulence: \(\theta \geq 0.5 \mathrm{arcseconds}\)
Higher turbulence: \(\theta \geq 2 \mathrm{arcseconds}\)

Using visible light (550 nm), at low turbulence:

\[ 0.5 \mathrm{arcseconds} = (0.5) \frac{2 \pi \mathrm{rad}}{360 * 60 * 60} = 2.424 \mu mathrm{rad} \]

(15.10)\[\begin{align} 2.424 \times 10^-6 &= \frac{550 \times 10^{-9}}{D} \\ D &= 0.22 m \end{align}\]

At high turbulence:

(15.11)\[\begin{align} D = \frac{550 \times 10^{-9}}{\frac{(2)(2 \pi)}{360 \cdot 60 \cdot 60}} = 0.0567 m \end{align}\]

Some existing telescopes:

Telescope	Diameter	Min Separation	Year Constructed
Keck (Hawaii)	10 m	\(0.07 \mu \mathrm{rad}\)
Gemini (Chile)	8.1 m	\( 0.08 \mu \mathrm{rad}\)
Bolshoi (Russia)	6 m	\( 0.1 \mu \mathrm{rad}\)
Mt. Wilson (California)	1.5 m	\( 0.4 \mu \mathrm{rad}\)	1908
Mt. Wilson (California)	2.54 m	\(0.26 \mu \mathrm{rad}\)	1917
Mt. Wilson (California)	5.08 m	\(0.13 \mu \mathrm{rad}\)	1949
Yerkes (Wisconsin)	1.01 m	\(0.66 \mu \mathrm{rad}\)	1895

All of these telescopes would be limited to \(\Delta \theta = 2.4 \mu \mathrm{rad}\) or a diameter of 0.22 m or 8.7 in.

Telescopes have a large diameter for greater light collection, rather than resolution.