1. Maxwell’s Equations#

1.1. Maxwell’s Equations in Vector Form#

We start with Maxwell’s equations:

(1.1)#\[ \nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t} \]
(1.2)#\[ \nabla \times \vec{H} = J + \frac{\partial \vec{D}}{\partial t} \]
(1.3)#\[ \nabla \cdot \vec{D} = \rho _v \]
(1.4)#\[ \nabla \cdot \vec{B} = 0 \]

In optics we do not use metal wires to create sources so we have a charge free and current source free media resulting in

(1.5)#\[ \rho _v = 0 \]
(1.6)#\[ \vec{J} = \sigma \vec{E} \]

The constitutive relations relate \(\vec{E}\) to \(\vec{D}\) and \(\vec{H}\) to \(\vec{B}\) as given by

(1.7)#\[ \vec{E} = \varepsilon _0 \vec{E} + \vec{P} \]
(1.8)#\[ \vec{H} = \frac{\vec{B}}{\mu _0} - \vec{M} \]

We often talk about linear, isotropic, and homogeneous (LIH) media.

1.2. Linear Media#

In general, \(\vec{P}\) depends on the magnitude of \(\vec{E}\) as given by

(1.9)#\[ \vec{P} = \varepsilon _0 \chi E + 2 d E^2 + 4 \chi^{(3)} E^3 + \ldots \]

If the higher order terms are insignificant then the material is linear

(1.10)#\[ \vec{P} = \varepsilon _0 \chi E \]
(1.11)#\[\begin{split} \begin{align} \begin{split} \vec{D} &= \varepsilon _0 \vec{E} + \varepsilon _0 \chi \vec{E} \\ &= \varepsilon (1 + \chi) \vec{E} \\ &= \varepsilon _0 \varepsilon _r \vec{E} \end{split} \end{align} \end{split}\]

The field of nonlinear optics will not be covered in this class. Applications for within nolinear optics, however, include electro-optic modulators, wavelength converters, etc.

1.3. Isotropic Media#

In general \(\varepsilon _r\) is a tensor (matrix) rather than a constant. The permittivity depends on the direction of the electric field.

Propagation in these anisotropic materials will not be covered in this class. Applications of anisotropic materials include polarization rotators, liquid crystals, etc.

1.4. Homogeneous Material#

A homogeneous material has no spatial variations in the material. All material has spatial variation for example at the atomic level there is a nucleus and electron clouds, etc. The homogeneity is only important relative to the wavelength. If the spatial variations are small compared to the wavelength then the material can be assumed as being effectively homogeneous.

If the media is completely homogeneous then there will be very little control over the field. For example, a lens is a spatial variation and thus a lens is a non-homogeneous material. So we will be analyzing propagation through non-homogeneous materials but we will look at propagation through homogeneous sections.

1.5. Solving Maxwell’s Equations#

Solving Maxwell’s equations directly is very hard so we need to make simplifications.

1.5.1. Low Frequency Domain (quasi-static)#

Spatial dimensions are much smaller than the wavelength.

(1.12)#\[ x, y, z \ll \lambda \]

Since the wavelength of optical signals is \(\sim 1 \mu m\), this domain is not feasible.

1.5.2. Resonant Domain#

Spatial dimensions are on the order of the wavelength.

  • Method of Moments (MOM)

  • Finite Element Method (FEM)

  • Finite Difference Time Domain (FDTD)

  • Finite Difference Frequency Domain (FDFD)

These methods are used in the analysis of optical systems but require very small computational grids. They are used most often in the analysis of guided wave optics where the sizes are small.

Integrated optics: 10mm X 10μm X 1μm Telescope: 1m X 1m X 1m

Dramatically different sizes.

1.5.3. High Frequency#

Spatial dimensions \(\gg\) wavelength.

This is very applicable to optics.

Broken into 2 parts: (1) physical optics, (2) geometrical optics

Geometrical Optics:

  • Ray tracing

  • Optical lens design

Physical optics:

  • Far-field beam propagation

  • Diffraction

  • Interference

1.6. Wave Propagation#

What we want to accomplish is to calculate the phase and amplitude of an optical wave at an arbitrary position after it has traveled through a set of optical components. The components can be apertures, lenses, gratings, etc.

The basic idea is to calculate the electric field at a particular plane given a known field at a different plane.

First of all, we assume that the fields are time harmonic as given by

(1.13)#\[ E ( x, y, z, t ) = \mathfrak{Re} \{ A (x, y, z) e^{j \omega t} \} \]

This assumes that the field only has a single wavelength. This constraint is called monochromatic. The analysis of non monochromatic waves is called coherence theory. This topic will not be covered in this class.

When describing the optical fields the complex form is often used with the \(\mathfrak{Re}\) and the \(e^{j \omega t}\) parts assumed.

The time harmonic form of Maxwell’s equations are given by

(1.14)#\[ \nabla \times \vec{E} = -j \omega \mu \vec{H} \]
(1.15)#\[\begin{split} \begin{align} \nabla \times \vec{H} &= \sigma \vec{E} + j \omega \varepsilon \vec{E} \\ &= ( j \omega \varepsilon + \sigma ) \vec{E} \\ &= j \omega \varepsilon _c \vec{E} \end{align} \end{split}\]
(1.16)#\[ \nabla \cdot \vec{D} = 0 \]
(1.17)#\[ \nabla \cdot \vec{B} = 0 \]

Combine the two curl equations to create one second order differential equation rather than two coupled first order differential equations.

(1.18)#\[\begin{split} \begin{align} \begin{split} \nabla \times (\nabla \times \vec{E}) &= \nabla \times (-j \omega \mu \vec{H}) \\ &= -j \omega \mu (\nabla \times \vec{H}) \end{split} \end{align} \end{split}\]

What assumption was made at this point? \(\mu\) does not have any spatial variation. This is valid since we are dealing with non-magnetic materials.

(1.19)#\[ \nabla \times (\nabla \times \vec{E}) = -j \omega \mu (j \omega \varepsilon \vec{E}) \]

Now we use the vector identity

(1.20)#\[ \nabla \times (\nabla \times \vec{E}) = \nabla ( \nabla \cdot \vec{E} ) - \nabla ^2 \vec{E} \]

For a linear homogeneous media

(1.21)#\[\begin{split} \begin{align} \begin{split} \nabla \cdot \vec{E} &= \nabla \cdot \frac{\vec{D}}{\varepsilon} \\ &= \frac{1}{\varepsilon} ( \nabla \cdot \vec{D} ) \\ &= 0 \end{split} \end{align} \end{split}\]

The wave equations becomes

(1.22)#\[\begin{split} \begin{align} \begin{split} \nabla \times (\nabla \times \vec{E}) &= -j \omega \mu (j \omega \varepsilon \vec{E}) \\ - \nabla ^2 &= \omega ^2 \mu \varepsilon \vec{E} \\ \nabla ^2 \vec{E} + k^2 \vec{E} &= 0 \end{split} \end{align} \end{split}\]

Since we do not have a homogeneous media, \(\nabla \cdot \vec{E} \ne 0\). The wave equation becomes (you will do this in homework)

(1.23)#\[ \nabla ^2 \vec{E} + 2 \nabla [ \vec{E} \cdot \nabla \ln(n) ] + k^2 \vec{E} = 0 \]

The second term can causes a coupling between the different components of the field. However, in most cases it is still rather small. In scalar theory this second term is neglected. This assumption required that the diffracting structures are large compared to the wavelength of the light. This is very valid for most structures such as apertures, lenses, etc.

The scalar approximation eliminates coupling between the various field components. The wave equation can then be used as a scalar equation. Each component of the electric and the magnetic field can be treated separately.

1.7. Scalar vs. Vector Wave Equation#

Are the different vector component of the fields independent? If they are then the wave equation can be broken up into three independent equations. Let’s look at the the wave equation in the cartesian coordinate system. The scalar wave equation

(1.24)#\[ \nabla ^2 \vec{E} + k^2 \vec{E} = 0 \]

becomes

(1.25)#\[\begin{split} \begin{align} \left( \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2} + \frac{\partial ^2}{\partial z^2} \right) E_x + k^2 E_x &= 0 \\ \left( \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2} + \frac{\partial ^2}{\partial z^2} \right) E_y + k^2 E_y &= 0 \\ \left( \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2} + \frac{\partial ^2}{\partial z^2} \right) E_z + k^2 E_z&= 0 \\ \end{align} \end{split}\]

So each equation is only in term of a single field component (\(E_x\), \(E_y\), or \(E_z\)). So the wave equation is actually just a scalar equation

(1.26)#\[ \nabla ^2 U + k^2 U = 0 \]

where \(U\) is either \(E_x\), \(E_y\), or \(E_z\).

If we take the vector wave equation

(1.27)#\[ \nabla ^2 \vec{E} + 2 \nabla [ \vec{E} \cdot \nabla \ln(n) ] + k^2 \vec{E} = 0 \]

and break it up into its vector components we get

(1.28)#\[ \nabla ^2 \vec{E} + 2 \nabla [ (E_x \hat{x} + E_y \hat{y} + E_z \hat{z}) \cdot (n_1 \hat{x} + n_2 \hat{y} + n_3 \hat{z})] + k^2 \vec{E} = 0 \]

The x component becomes

(1.30)#\[\begin{split} \frac{\partial ^2 E_x}{\partial x^2} + \frac{\partial ^2 E_y}{\partial y^2} + \frac{\partial ^2 E_z}{\partial z^2} ) + \frac{\partial}{\partial x} (E_x n_1 + E_y n_2 + E_z n_3) + k^2 E_x = 0 \\ \end{split}\]

Now we have an equation with \(E_x\), \(E_y\), and \(E_z\) components. Thus, we have coupling between the various vector components. The equation can no longer be treated as a scalar equation. You can get coupling between polarization components.

1.8. Energy Flow#

The instantaneous power crossing a unit area is the Poynting vector \(\vec{S}\) as given by

(1.30)#\[ \vec{S} = \vec{E} \times \vec{H} \]

The intensity is defined as the time averaged power crossing a unit area

(1.31)#\[ \mathrm{Intensity} = I = \langle \vec{S} \rangle = \frac{1}{T} \int_0^T \vec{S} dt \]

1.9. Elementary Waves#

There are a variety of complex fields that satisfy the time harmonic scalar wave equation. Some common notation is

(1.32)#\[\begin{split} \begin{align} \vec{r} &= x \hat{x} + y \hat{y} + z \hat{z} \\ \vec{k} &= k_x \hat{x} + k_y \hat{y} + k_z \hat{z} \end{align} \end{split}\]

1.9.1. Plane Waves#

  • The amplitude does not change with distance

  • The phase is constant over a plane

(1.33)#\[ \vec{E} (x, y, z) = \vec{E}_0 e ^{j \vec{k} \cdot \vec{r}} \]
(1.34)#\[ \vec{H} (x, y, z) = \vec{H}_0 e ^{j \vec{k} \cdot \vec{r}} \]

where

(1.35)#\[ \vec{E}_0 \perp \vec{k} \]
(1.36)#\[ \vec{H}_0 \perp \vec{k} \]
(1.37)#\[ \vec{E}_0 \perp \vec{H}_0 \]
(1.38)#\[ \frac{ | \vec{E}_0 | }{ | \vec{H}_0 | } = \sqrt{ \frac{\mu}{\varepsilon} } = \frac{377}{n} \]

1.9.2. Spherical Waves#

  • The field decreases with distance away from the focal point ar \(1/r\).

  • The phase is constant over a spherical surface

(1.39)#\[ \vec{E} = \frac{\vec{E}_0}{r} e ^{j k r} \]

1.9.3. Gaussian Waves#

There is also a common solution to the paraxial wave equation.

(1.40)#\[ \vec{E} = \frac{\vec{E}_0}{r} e ^{j k z} e ^{j k \frac{x^2 + y^2}{2z}} \]

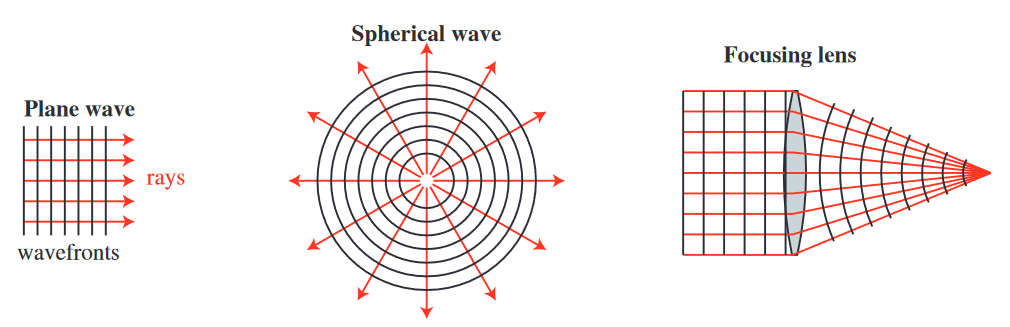
1.10. Wavefront#

A wavefront is a surface of equal phase. For a plane wave it is a plane and for a spherical wave it is a sphere. The separation between wavefronts is the wavelength of the optical signal.

Huygens Principle

(or, the Huygens-Fresnel prinicple) states that each point on a wave front generates a spherical wave. The envelope of these secondary waves constitutes a new wavefront. Their superposition constitutes the wave in another plane.

1.11. Geometrical Optics#

In the geometrical optics approximation a ray is used to represents the normal to a wavefront. This is the high frequency limit. It ignores diffraction.

Each ray corresponds to a bucket of power. The spread of the rays corresponds to a decrease in power density. Ray tracing is primarily done in incoherent systems, where if two rays hit it just has twice the power. When a ray hits an interface Snell’s law is aplied and then the ray travels in a straight line in between interfaces.

With ray tracing a system can be designed in which all of the rays pass through an arbitrarily small spot. Using the light bucket analysis, this would mean that the light in this spot would approach infinity. Since this is not reality, ray tracing is not valid at a focal spot. If the rays are all traveling in the same direction then the size of the optical beam would remain the same size no matter how far the beam propagated. Again this is not realistic, so ray tracing is not valid in this case.

In addition to designing optical systems, ray tracing is also useful in analyzing light scattering, multiple reflections and other stray light cases. It can also be used in analyzing light pipes and illu- minators (headlight, etc). It is only valid if the light pipe is large in comparison to the wavelength.

Geometrical Optics Diagram