Problem Set 7: Fields

Problem Set 7: Fields#

Write down (a) the electric field and (b) the magnetic field vector in phasor form for a plane wave with frequency 2.4 GHz, propagating in the \(\hat{x}+\hat{y}\) direction, linearly polarized in the z direction, and with an irradiance of \(2 W/m^2\).
DIRECTV uses the Ka frequency band (26.5 GHz – 40 GHz). It uses an off-axis parabolic dish with a circular diameter of 0.5m (see Fig. 5).

Fig. 5 DIRECTV’s dish.#

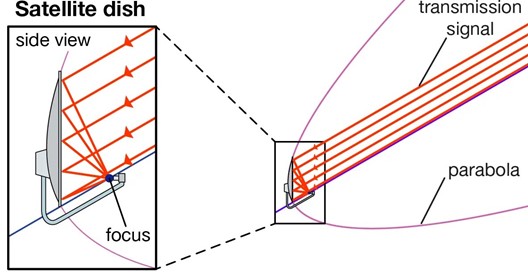
Fig. 6 An off-axis parabolic dish.#

Fig. 7 shows that the source plane is defined as a plane perpendicular to the propagation direction. If the total power of the beam is 1W and the shape of the beam is a cosine with zero electric field at the edge of 0.5m diameter dish, what is the peak irradiance?

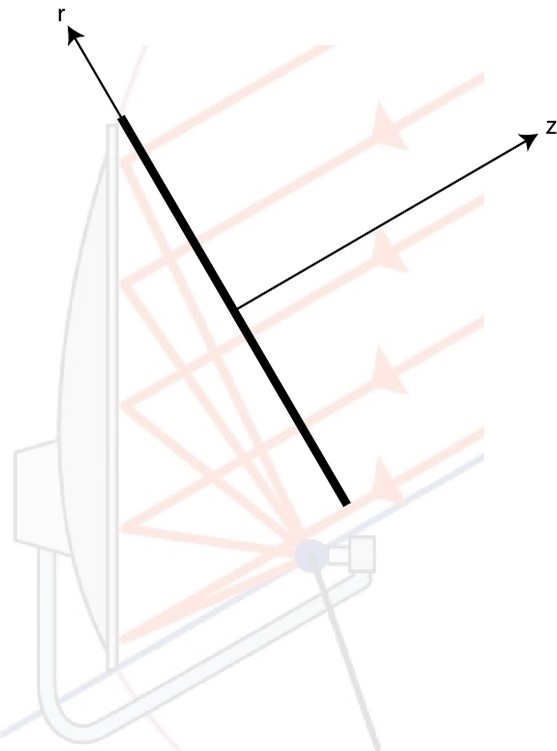
Fig. 7 The source plane is defineed as a plane perpendicular to the propagation direction.#
If the electric field at a square aperture is given by \(\psi \left( x,y,z = 0^- \right) = 5 \exp{\left(-\frac{x^2+y^2}{10}\right)}\) and the aperture has a width of 20, what is the electric field at the position (5,7,10)? Set up the integral but don’t solve it. Use the diffraction integral \(\psi \left( P_o \right) = \frac{z}{i\lambda} \int{ \int \psi \left( P_1 \right) \frac{\exp \left( ikr \right) }{r^2} dS}\).