Problem Set 1: Geometrical Optics#
Start with the general form of the electric field \(\vec{E} = \vec{E}_0 \exp (-j k \phi)\), where \(\vec{E}\), \(E_0\), and \(\phi\) all vary with position. Show that with the geometrical optics approximation \((\lambda \to 0, k \to \infty)\) Gauss’s law becomes \((\nabla \cdot \vec{E} = 0)\).
A lifeguard is standing at the point A \((0, 0)\) and a person is drowning at the point B \((x_0, y_0)\), as shown in Fig. 1. The lifeguard has a running speed of \(v_1\) and swimming speed of \(v_2\) \((v_1 \gt v_2)\). What is the quickest path for the lifeguard to take?

Fig. 1 A pool.#
Book Problem 1.7
Book Problem 2.1
Book Problem 2.2 (use \(c_1 = 1.4\))
Book Problem 2.4
A ray is incident onto a 45-45-90 prism at an angle of \(20^\circ\) (see Fig. 2). If the two legs are mirror coated, what is the direction of the beam after passing through the prism?

Fig. 2 A 45-45-90 prism.#
A beam is refracted through a prism shown in Fig. 3.
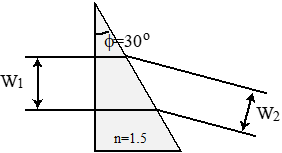
Fig. 3 A 30-60-90 prism.#
a. What is the ratio of the beam sizes (\(W_2 / W_1\))?
b. A collimated beam has an elliptical cross section, with a semiaxis ratio of 2:1. Design a prism system that can transform the beam to be circular.
Solutions
Problem 1
Some hidden toggle content!
Great!
Problem 2
Some hidden toggle content!
Great!
Problem 3
Some hidden toggle content!
Great!
